Complexidade de Algorítmos
No primeiro post do blog , eu dissertei um pouco sobre o conceito de algorítmos, sua importância como base fundamental no desenvolvimento de software, suas características e como eles são sequências de passos para resolver um problema, seja problema de codificação ou cozinhar, ou fazer qualquer tarefa, os algorítmos serão esses passo a passos que dada uma entrada, irá fornecer uma saída desejada. Antes de mostrar exemplos de algorítmos clássicos que serão uma porta de entrada para construção dos seus próprios algorítmos, quero falar sobre um conceito fundamental: Complexidade de algorítmos.
Quando começamos a programar, nosso foco geralmente está em “fazer funcionar”, e está tudo bem, acredito que essa seja a maneira correta de começar qualquer código, depois inserimos camadas de fatoração e otimização, mas maturar isso acredito que seja fundamental, ou seja, escrever um código que funciona não é o suficiente, ele precisa ser eficiente, previsível e escalável e adicionaria também manutenível.
Quem estudou ciências da computação visitou os conceitos de complexidade de algoritmo que representa quanto tempo (time complexity) e quanta memória (space complexity) ele precisa à medida que o tamanho da entrada (representada por n) cresce.
Pense n como o número de elementos com os quais seu algoritmo trabalha: usuários em um banco de dados, pixels em uma imagem, posts em uma rede social, etc. Logo, o objetivo principal da análise de complexidade é prever o comportamento de um algoritmo para entradas muito grandes, sem precisar implementá-lo e testá-lo fisicamente. É uma análise do pior cenário possível.
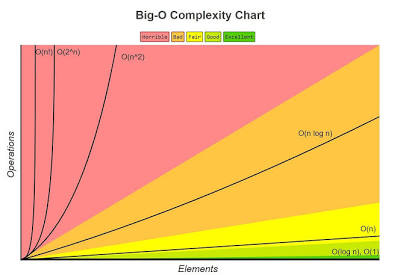
A Notação Big O
A ferramenta mais comum para expressar complexidade é a Notação Big O. Ela descreve o pior cenário de crescimento de um algoritmo quando a entrada tende ao infinito. Ela nos dá uma abstração de como o tempo de execução ou o uso de memória cresce em relação ao tamanho da entrada n.
Quando dizemos que um algoritmo é O(n), estamos dizendo que seu tempo de execução cresce linearmente com n. Se n dobra, o tempo também dobra.
Vamos explorar as complexidades mais comuns, da mais eficiente para a menos eficiente.
O(1) - Tempo Constante
O tempo de execução é constante, independentemente do tamanho da entrada.
1
2
3
def get_first_element(items)
items[0] # Sempre leva o mesmo tempo, não importa se a lista tem 10 ou 10 milhões de itens.
end
O(log n) - Complexidade Logarítmica
O tempo cresce logaritmicamente, é extremamente eficiente. O tempo de execução cresce muito lentamente mesmo com n crescendo drasticamente. A busca binária é o exemplo clássico: a cada iteração, dividimos o problema pela metade.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def busca_binaria(lista_ordenada, alvo)
esquerda = 0
direita = lista_ordenada.length - 1
while esquerda <= direita
meio = (esquerda + direita) / 2
if lista_ordenada[meio] == alvo
return meio
elsif lista_ordenada[meio] < alvo
esquerda = meio + 1
else
direita = meio - 1
end
end
-1
end
O(n) - Tempo Linear
O tempo de execução cresce proporcionalmente ao tamanho da entrada. Percorrer todos os elementos de uma lista é O(n).
1
2
3
4
5
6
7
def encontrar_maximo(lista)
maximo = lista[0]
lista.each do |elemento| # Percorre todos os n elementos
maximo = elemento if elemento > maximo
end
maximo
end
O(n log n) - Complexidade Linearítmica
Comum em algoritmos de ordenação eficientes como Merge Sort e Quick Sort. É mais rápido que O(n²) mas mais lento que O(n).
O(n²) - Complexidade Quadrática
O tempo cresce exponencialmente com o quadrado da entrada. Loops aninhados geralmente indicam essa complexidade.
1
2
3
4
5
6
7
8
9
10
11
def bubble_sort(lista)
n = lista.length
(0...n).each do |i| # Loop externo: n iterações
(0...(n - i - 1)).each do |j| # Loop interno: n iterações
if lista[j] > lista[j + 1]
lista[j], lista[j + 1] = lista[j + 1], lista[j]
end
end
end
lista
end
O(2ⁿ) - Complexidade Exponencial
Extremamente ineficiente para entradas grandes. Comum em soluções recursivas ingênuas, como calcular Fibonacci sem memoização.
Complexidade de Espaço
Existe também enquanto a complexidade de espaço que mede quanta memória adicional o algoritmo precisa. Um algoritmo pode ser rápido O(n) mas usar muita memória O(n), ou pode ser mais lento O(n²) mas usar pouca memória O(1). Essa é o famoso trade-off entre tempo e espaço. Um algoritmo pode ser mais rápido porque usa mais memória (como uma tabela de cache), ou pode ser mais econômico em memória mas levar mais tempo para executar.
Ótimo, entendemos o que são, onde comem e onde dormem complexidade de tempo e espaço de algorítmos, sabemos que temos hoje temos processadores multicore, SSDs rápidos e GPUs capazes de trilhões de operações por segundo que permitem rodar algoritmos antes considerados lentos, mesmo assim, complexidade é um assunto de fundamento importante, mas é preciso entender caso a caso, e ter um pensamento crítico de um bom engenheiro de software, a primeira coisa é saber usar algorítmos eficientes quando necessário sistemas que precisam de um pouco maior de volume ou alta concorrência, para a maioria dos outros casos menores uma solução simples e clara pode ser mais importante do que otimizar Big-O, então não complicar demais prematuramente é uma lição que você deve usar a vida toda para ser um bom programador, antes de tentar otimizar meça tudo, tenha dados concretos e específicos para uma boa otimização, e entender o cenário real do que tentar implementar algo só porque é bonito ou teoricamente mais otimizado.
Na minha concepção um bom programador toma boas decisões conscientes que impactam diretamente na complexidade do código, como: Usar estruturas de dados apropriadas: hash tables para buscas O(1), árvores balanceadas para O(log n) , Saber usar memoização e programação dinâmica para trabalhos repetidos ou Dividir para conquistar quando necessário para quebrar problemas em subproblemas menores.
O segredo está em entender os fundamentos profundamente para poder fazer essas escolhas conscientemente, não por ignorância.